Mronne's Blog

（十一）SVM(Support Vector Machine)

 
  • 2020年 03月07日

Hinge Loss Kernal

1.传统二分类问题

  • 但在实际操作过程中，$\delta$函数不可微
  • 采用近似损失函数$l(f(x^n),\hat(y)^n)$进行模拟

损失函数

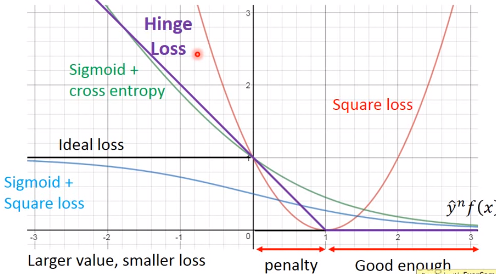上图中各损失函数为：

  • Ideal Loss:$\delta(f(x^n),\hat{y}^n)$，原则上，$\hat{y}^nf(x^n)$越大，损失函数值应该越小
  • Square Loss:$l\left(f\left(x^{n}\right), \hat{y}^{n}\right)=\left(\hat{y}^{n} f\left(x^{n}\right)-1\right)^{2}$，表现很差
  • Sigmoid+Square Loss：$l\left(f\left(x^{n}\right), \hat{y}^{n}\right)=\left(\sigma\left(\hat{y}^{n} f(x)\right)-1\right)^{2}$，与理想损失函数较为接近，但在负数部分梯度变化很小，不适合训练
  • Sigmoid+交叉熵：$l\left(f\left(x^{n}\right), \hat{y}^{n}\right)=\ln \left(1+\exp \left(-\hat{y}^{n} f(x)\right)\right)$，是理想损失函数的上界，训练表现好于平方差函数
  • Hinge Loss：$l\left(f\left(x^{n}\right), \hat{y}^{n}\right)=\max \left(0,1-\hat{y}^{n} f(x)\right)$，对离群点训练结果比较鲁棒

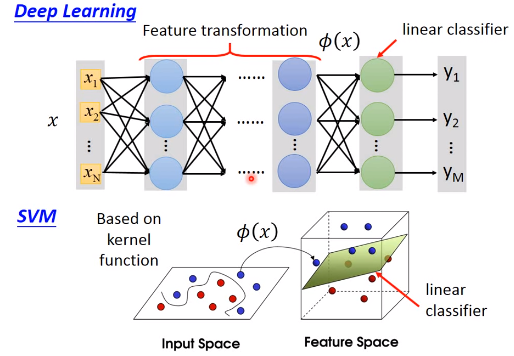
2.Linear SVM

2.1 Function（Model）

f(x)=\sum_{i} w_{i} x_{i}+b=\left[\begin{array}{l}
{w} \\
{b}
\end{array}\right] \cdot\left[\begin{array}{l}
{x} \\
{1}
\end{array}\right] = w^Tx

2.2 Loss Function

L(f)=\sum_{n} l\left(f\left(x^{n}\right), \hat{y}^{n}\right)+\lambda\|w\|_{2}

l\left(f\left(x^{n}\right), \hat{y}^{n}\right)=\max \left(0,1-\hat{y}^{n} f(x)\right)
  • 上述的损失函数均为凸函数
  • 对于Hinge Loss存在不可微的情况，可人为设定微分

2.3 梯度下降求解

2.4 带有正则化项的梯度求解

当存在正则化项，损失函数为

L(f)=\sum_{n} \max \left(0,1-\hat{y}^{n} f(x)\right)+\lambda\|w\|_{2}
  • 令$\varepsilon^{n}=\max \left(0,1-\hat{y}^{n}f(x)\right)$,则$\varepsilon^{n}$满足以下条件：
\begin{aligned}
&\varepsilon^{n} \geq 0\\
&\varepsilon^{n} \geq 1-\hat{y}^{n} f(x) \mapsto \hat{y}^{n} f(x) \geq 1-\varepsilon^{n}
\end{aligned}
  • 要想最小化$L(f)$，$\varepsilon^{n}$也要尽可能小
  • $\varepsilon^{n}$最小的办法是令$\varepsilon^{n}=\max \left(0,1-\hat{y}^{n}f(x)\right)$，此时该值为$\varepsilon^{n}$的下界
  • 零``

2.5 Dual Representation

  • 假如损失函数为Hinge Loss，$c^n(w)$在某些区域为0，因此$\alpha_n^*$是稀疏的，对于权值$\alpha_n^*$部位0的$x^n$即为Support Vectors
  • 经过数学变形可将损失函数变形为K函数，此时向量x的值并不关键，重要是求解K(x,z)，此即Kernal Trick

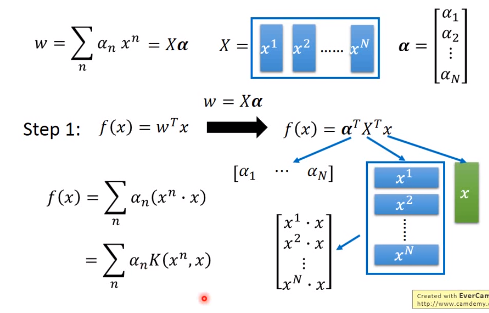
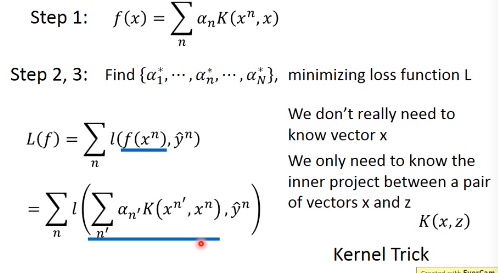
2.6 Kernel Trick

  • 假如对x，z分别进行线性变换后结果是$\phi(x)$，$\phi(z)$
  • 通过如下推导 
    K(x, z)=\phi(x) \cdot \phi(z) = (x \cdot z)^2
  • 直接计算$K(x,z)$要比先进行特征变换，再进行内积速度要快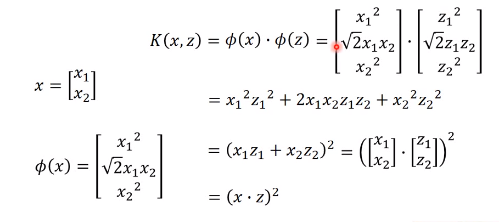

2.6.1 Radial Basis Function Kernel

在无穷对维平面进行操作

\begin{array}{l}
{K(x, z)=\exp \left(-\frac{1}{2}\|x-z\|_{2}\right)=\phi(x) \cdot \phi(z) ?} \\[0.6em]
{=\exp \left(-\frac{1}{2}\|x\|_{2}-\frac{1}{2}\|z\|_{2}+x \cdot z\right)} \\[0.6em]
{=\exp \left(-\frac{1}{2}\|x\|_{2}\right) \exp \left(-\frac{1}{2}\|z\|_{2}\right) \exp (x \cdot z)=C_{x} C_{z} \exp (x \cdot z)}\\[0.6em]
{=C_{x} C_{z} \sum_{i=0}^{\infty} \frac{(x \cdot z)^{i}}{i !}}
\end{array}

2.6.2 Sigmoid Kernel

K(x,z)=tanh(x \cdot z)

2.6.3 直接设计K(x,z)

  • 当x是结构化对象时，很难设计$\phi(x)$，但可以直接设计$K(x,z)$
  • $K(x,z)$和计算相似度很相似

3.SVM相关方法

搜索