综述

• 在平面上移动时，机器人有三个状态量$(x,y,\theta)$
• 理论上，应该做三维轨迹规划$(x(t),y(t),\theta(t))$
• 实际上，只需要做二维轨迹规划$(x(t),y(t))$或者 $(v(t),w(t))$

$$\theta(t)=\operatorname{acttan} \frac{\dot{y}(t)}{\dot{x}(t)}=\operatorname{acttan} \frac{y(t+1)-y(t)}{x(t+1)-x(t)}$$ $$\left\{\begin{array}{c} \dot{\theta}(t)=w(t) \\ \dot{x}(t)=v(t) \cos \theta(t) \\ \dot{y}(t)=v(t) \sin \theta(t) \end{array}\right.$$

方法

• $x(t),y(t)$
  • 完整机器人 独立规划、时间同步
  • 非完整机器人 图形搜索法
• $v(t),w(t)$
  • 参数优化法、反馈控制法

图形搜索法

• 根据路径搜索经过（近似经过）路径点且满足运动学约束的图形曲线

  Dubins曲线、Reeds-Shepp曲线、Balkcom-Mason曲线 回旋曲线、多项式曲线、贝塞尔曲线、样条曲线

• 采用运动基元。从起始点开始不断搜索由运动基元组合而成的最佳单词来获得最优轨迹
• 可以实现位置的连续平滑，充分考虑了机器人的运动学约束和时间最优要求
• 存在问题
  • 如何构建单词和搜索最佳单词
  • 运动基元方式实际是对状态空间和控制空间进行了离散化，直接导致空间分辨率降低，能达到的边界状态只是预定义单词能够达到的状态

参数优化法

• 对移动机器人参考点的速度控制律进行参数化表示
• 对平面机器人对速度控制量$v,w$单独规划控制
• 为满足起始点、终止点的边界约束，利用运动学/动力学模型合成各个速度控制量，得到速度控制的合成效果
• 根据合成效果和期望效果的差异，采用数值法搜索得到满足边界条件的最优参数，确保满足空间位置约束

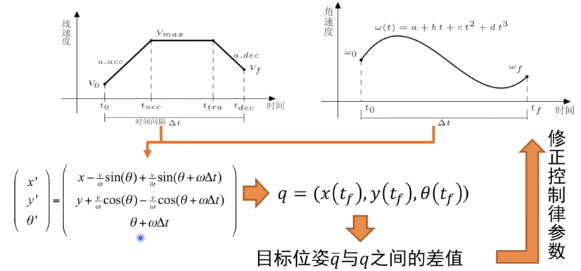
v的一维轨迹参数化表示

• $v_0$,$v_1$由任务给定
• $a_a$,$a_d$利用机器人最大加速度和最大减速度确定
• $v_c$由机器人最大速度确定
• 唯一需要确定的参数是$\Delta t$

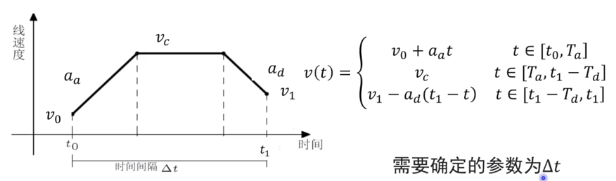
w的一维轨迹参数化表示

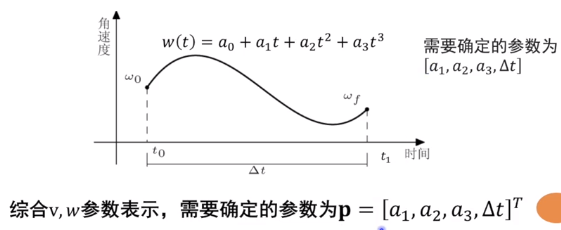
流程

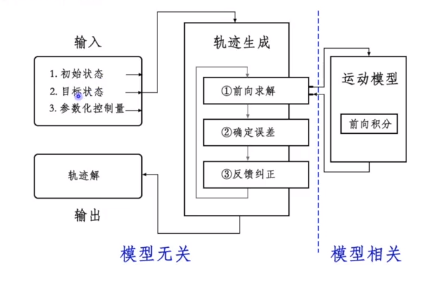
• 数值优化求解与初值有关系，存在局部最优
• 实际应用时，通常预先构造初始猜测查找表（或者构建神经网络），建立边界约束与控制律参数之间的映射关系
• 根据实际边界条件查表，以表中值作为初值，迭代计算得到最优控制律参数

比较

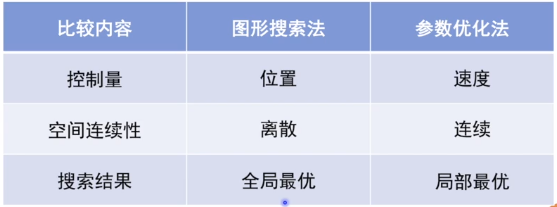
反馈控制法

• 根据当前状态与目标状态之间的差异，来生成减少这种差异的控制律