RRT(Rapid-Exploring Random Tree)
RRT即通过扩张树的方式寻找一条可行路径
基本思想
- 连通图采用树的形式,在空间中随机采样、连接树中最近节点的方式拓展树
- 考虑机器人的运动执行能力
- 通过树结构可直接回溯得到路径
流程
- 以起点为根节点,建立搜索树
- 对树进行扩张:
- 随机采样:在状态空间中,随机采样一个状态,称为$q_{sample}$
- 寻找最近点:在现有搜索树中查找与$q_{sample}$距离最近的点$q_{closest}$
- 确定扩张新节点:依据$q_{sample}$和$q_{closest}$确定新的树扩张节点$q_{new}$
- 二维路径规划可根据$q_{sample}$和$q_{closest}$的方向结合步长确定新的节点$q_{new}$
- 高维路径规划可考虑机器人的系统状态方程,以$q_{sample}$和$q_{closest}$构建新的输入$\mathbf{u}$,以$q_{closest}$作为当前状态$\mathbf{x}$,根据系统的状态方程$\dot{x}=f(x, u)$,得到下一个状态即新的扩张节点$q_{new}$
- 判断新节点:判断$q_{closest}$和$q_{new}$是否是无碰路径,且$q_{new}$不在搜索树中
- 对$q_{closest}$和$q_{new}$逐个取点,看是否在障碍物内部
- 把新节点加入树中:把$q_{new}$加入到搜索树中
- 终止条件:
- $q_{new}$已经到达终点
- 失败尝试达到最大次数,搜索树的规模已经足够大,没有可行路径,返回fail
- 确定可行路径:如果确定规划成功,返回从初始状态到终点的节点路径
伪代码
function BuildRRT(qinit, K, Δq) //建立搜索树
T.init(qinit) //初始化
for k = 1 to K
q_sample = Sample() -- 在位形空间中随机采样
qnearest = Nearest(T, qrand) //寻找最近点
if Distance(qnearest, qgoal) < Threshold then
return true
qnew = Extend(qnearest, qrand, Δq) //确定扩张新节点
if qnew ≠ NULL then //判断新节点是否满足要求
T.AddNode(qnew) //把新节点加入树中
return false


分析
- 影响规划收敛速度的三个因素:
- 随机状态的采样位置
- 在搜索树中查找与随机状态距离最近的节点
- 新生成节点的防撞检测
不足与改进
- 当空间中包含大量的障碍物,或者狭窄的通道约束时,算法的收敛速度很慢,有时甚至无法找到可行解。
- 针对RRT的改进,可以从以下几方面入手
- 如何进行随机采样
- 如何定义和查找最近点
- 如何进行树的扩张
确定最近距离和查找最近点
- 计算距离最简单的方法是欧氏距离,但在很多场景下此种距离并不可行
- 另一种可行方法是对距离的不同分量进行加权平均,不同分量的重要程度用权重大小表示
- 寻找最近点有很多可行的算法,如K-D树,Hash算法等
确定路径
- 一种方法是计算Xnearest和它的最近边之间的距离向量,取向量与最近边的交点加入连通图中
- 将离散化的节点链接到最近的节点上,可以将顶点附加到最近的节点上。
RRG(Rapidly Exploring Random Graph)
- 针对RRT产生的路径不是渐进最优的问题进行改进
原理
使用结构$k=(S,S_0,T,L)$来表示系统的性能。其中$S$表示状态集合,%S_0%是初始状态集合,$T \subseteq S \times S$代表过渡关系,$L$是标记函数,用于将每个状态映射到原子命题集。
- 对每个确定的新节点把它和它附近一定范围内的节点都连接起来,而不是只连接最近节点。如下图所示
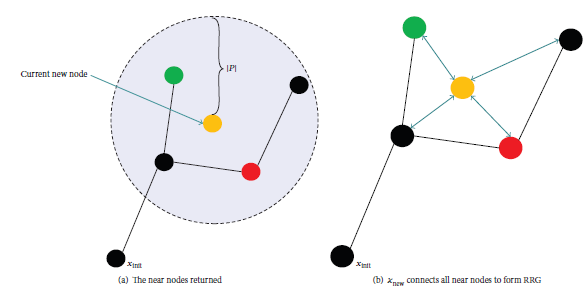
算法流程如下

- RRG通过将新节点周围一定范围的节点连接起来,构成一个graph,从而增大了候选路径的范围。可几乎保证算法收敛到最优解。
- 但是在构建的图的基础上还需要寻路算法才能找到最优路径。
RRT*
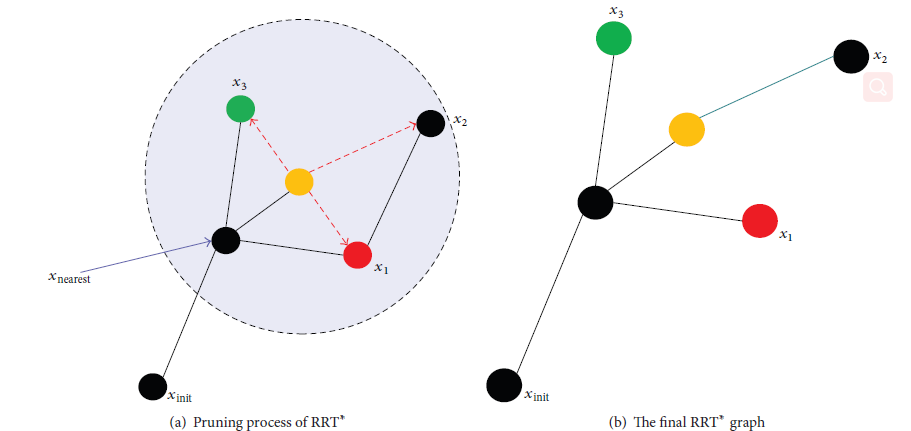
修剪与重新连接
针对RRT随机性扩展步长小导致的路径曲折,成本较高的问题,进行改进。
- 寻找树中新节点邻域内到新节点路径最短的节点,建立连接,加入树集合
- 对树中新节点邻域内的节点进行判断,如果从新节点到该节点形成的路径优于现有树中路径,则将该节点的父节点修改为新节点
原理
- 定义一个cost function cost(p)表示从初始状态$x_{init}$到任意状态%p \in P%的代价,设置$cost(x_{init})$为0
- RRT* 首先找到最近的状态和相邻的状态$X_{near}$,然后将最近的状态添加到树中,并在存在最小代价连接的情况下添加最小代价连接
- RRT* 通过连接$X_{new}$来消除开销较大的连接
流程
- 扩展树部分的算法流程如下

- 前几步采样扩展步长与之前类似
- 只是当扩展出新步长的时候,用near函数求邻近点,遍历邻近点集合,寻找花费代价最小的节点$q_{min}$,把$(q_{min},q_{new})$加入到边集合中
- 最后进行进一步的回溯,如果存在一条路径经过$q_{new}$到达$q_{near}$花费的代价小于$q_{near}$的parent到达$q_{near}$的代价,说明原来到达$q_{near}$的代价不是最优的,需要选择$q_{new}$到达$q_{near}$的路径作为新路径。
- 对所有的邻近点集合内的点都做相同的操作,经过N次迭代得到接近最优的次优路径了。
双向RRT
针对RRT扩展偏向于空间未探测的部分,但不是偏向目标点,当环境复杂时计算效率较低。采用双向RRT的方式从起始点和目标点分别扩张,提高计算效率。
