A* 算法是在形成的路径连通图上寻找最佳路径。在连通图上进行路径搜索有以下几种算法:
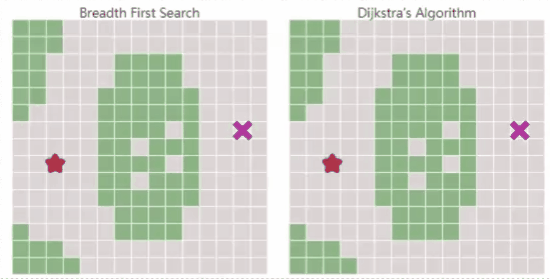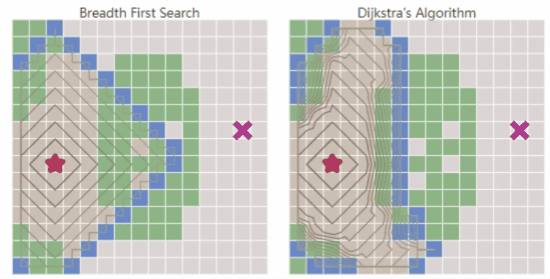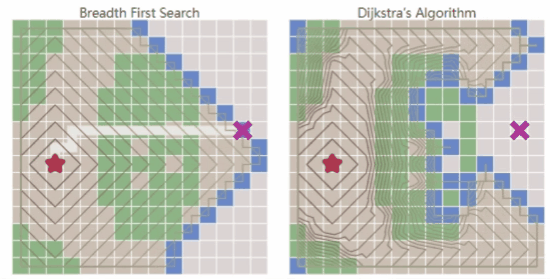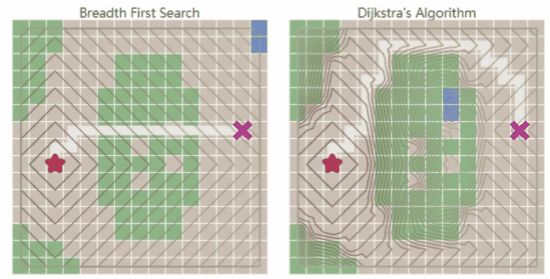
- 广度优先搜索(Breadth First Search):在所有方向上均匀探索,适用于地图所有代价都一致的场景。可覆盖地图所有区域,但搜索速度较慢。
- Dijkstra’s Algorithm:优先考虑低代价的路径进行探索,可以找到去所有方向的路径,适用于不同区域不同代价的场景。
- A* :A* 算法是Dijkstra’s的变种,考虑了距离目标的代价,可快速找到最短路径。
广度优先搜索 Breadth First Search
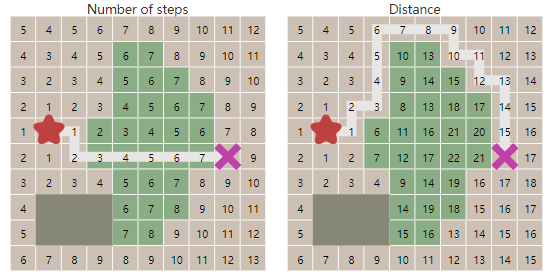
- 广度优先搜索的核心在于对地图进行广度遍历即探索边界的扩张,对于栅格地图常常称为“泛洪”,如下图所示:

地图探索
编写程序实现对地图的探索,步骤如下
- 定义探索的边界队列 frontier,重复如下步骤直至其为空
- 从边界队列frontier中选择一个location,将其移除
- 对location的周围邻居neighbors进行检查。 如果它不在visited set中,就将其加入到frontier里,并加入到visited set中
python实现广度地图探索代码如下
frontier = Queue()
frontier.put(start )
visited = {}
visited[start] = True
while not frontier.empty():
current = frontier.get()
for next in graph.neighbors(current):
if next not in visited:
frontier.put(next)
visited[next] = True确定路径
- 上述过程是对整个地图的探索,但要想找到路径需要保存当前节点的父节点,到达终点后回溯即可确定路径。即确定一个新数组came_from,保存当前节点的父节点。
python 代码如下
frontier = Queue()
frontier.put(start )
came_from = {}
came_from[start] = None
while not frontier.empty():
current = frontier.get()
for next in graph.neighbors(current):
if next not in came_from:
frontier.put(next)
came_from[next] = current
确定路径时只需回溯即可
current = goal
path = []
while current != start:
path.append(current)
current = came_from[current]
path.append(start) # optional
path.reverse() # optional
Early Exit
- 在实际情况中无需遍历所有的地图,在到达终点后及时停止可减少程序运行时间。
frontier = Queue()
frontier.put(start )
came_from = {}
came_from[start] = None
while not frontier.empty():
current = frontier.get()
if current == goal:
break
for next in graph.neighbors(current):
if next not in came_from:
frontier.put(next)
came_from[next] = current
Dijkstra’s Algorithm
- 假如地图中不同的区域存在不同的代价,广度优先搜索明显不适用了。
- 在此时需要采取记录到当前点总共花费的代价,如果该位置的新路径比之前的最佳路径的代价更低,将采用此条路径。
frontier = PriorityQueue() # 优先级队列 依据代价大小进行顺序存储
frontier.put(start, 0)
came_from = {}
cost_so_far = {}
came_from[start] = None
cost_so_far[start] = 0
while not frontier.empty():
current = frontier.get()
if current == goal:
break
for next in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if next not in cost_so_far or new_cost < cost_so_far[next]:
cost_so_far[next] = new_cost
priority = new_cost
frontier.put(next, priority)
came_from[next] = current
- Dijkstra’s Algorithm实际是改变了边界扩展的方式,相比于广度优先搜索,考虑了地图代价,能找到最优路径。
启发式搜索
- 广度优先搜索和Dijkstra算法中,边界向各个方向扩展。
- 为提高算法的搜索速度,考虑让边界尽可能向着目标方向扩展,即定义一个启发式函数表明与目标之间的距离:
def heuristic(a, b):
# Manhattan distance on a square grid
return abs(a.x - b.x) + abs(a.y - b.y)
Greedy Best First Search
- 优先考虑距离目标近的区域
frontier = PriorityQueue()
frontier.put(start, 0)
came_from = {}
came_from[start] = None
while not frontier.empty():
current = frontier.get()
if current == goal:
break
for next in graph.neighbors(current):
if next not in came_from:
priority = heuristic(goal, next)
frontier.put(next, priority)
came_from[next] = current
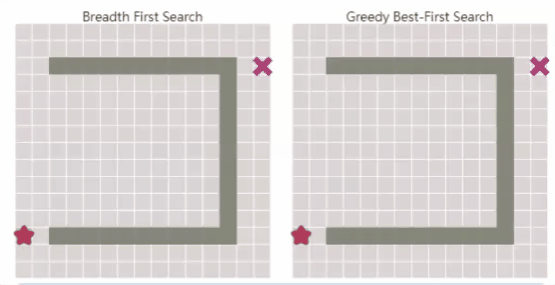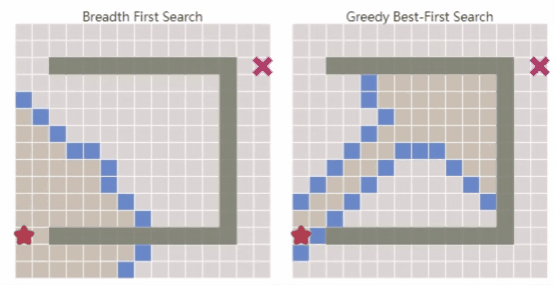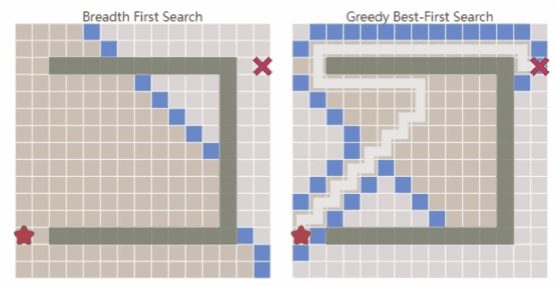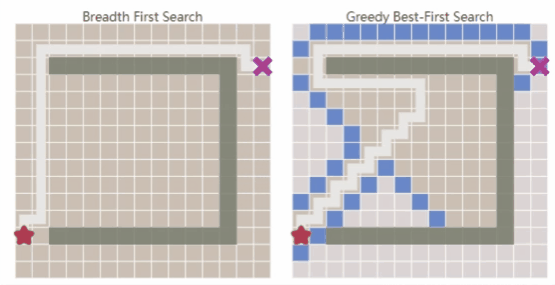
相比于广度优先搜索,能快速找到通往目标的路径,但在复杂环境中可能无法得到最优解。
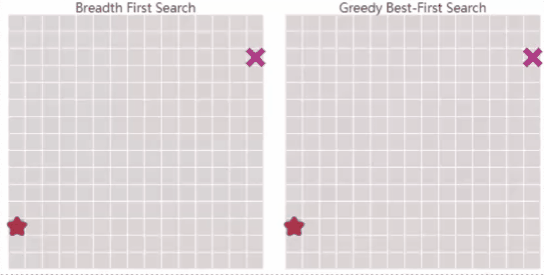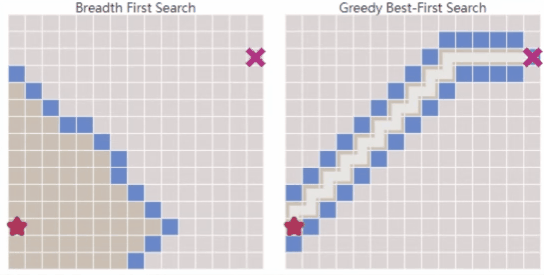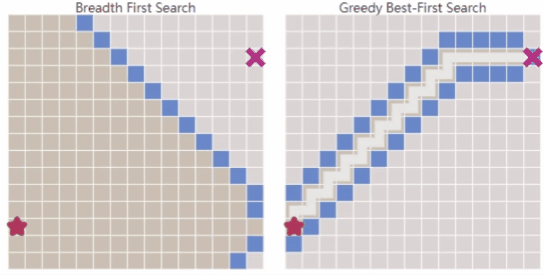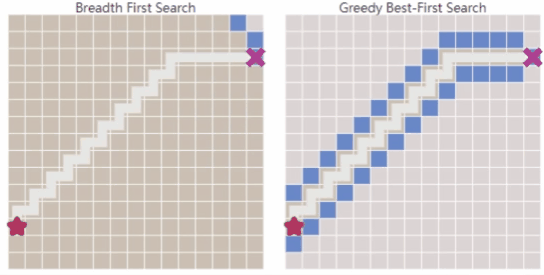
A*算法
- 综上所述,Dijkstra算法可以很好地找到最短路径,但是它会浪费时间在不太有前途的方向上。Greedy Best First Search在有希望的方向探索,但它可能找不到最短路径。
- A*算法将这两种算法结合到一起,考虑从start到current location的实际代价,以及从current location到goal的估计代价。
frontier = PriorityQueue()
frontier.put(start, 0)
came_from = {}
cost_so_far = {}
came_from[start] = None
cost_so_far[start] = 0
while not frontier.empty():
current = frontier.get()
if current == goal:
break
for next in graph.neighbors(current):
new_cost = cost_so_far[current] + graph.cost(current, next)
if next not in cost_so_far or new_cost < cost_so_far[next]:
cost_so_far[next] = new_cost
priority = new_cost + heuristic(goal, next)
frontier.put(next, priority)
came_from[next] = current
总结
- 最优路径:广度优先搜索和Dijkstra算法保证在给定输入图的情况下找到最短路径。Greedy Best First Search有时无法找到最佳路径。如果启发式函数永远不大于真实距离,则A*一定能找到最短路径。随着启发式函数变小,A*变成了Dijkstra算法。当启发式变大时,A*变成Greedy Best First Search。
- 时间:减少图的大小有助于所有的图搜索算法。之后,使用最简单的算法;更简单的队列运行得更快。Greedy Best First Search通常比Dijkstra算法运行得快,但不会产生最优路径。对于大多数寻路需求来说,A*是一个不错的选择。