行车图法

1.基本思想

• 基于障碍物的几何形状对位形空间进行分解，将自由空间的连通性用一维曲线的网格表示。
• 加入起始点和目标点后，在该一维无向连通图中寻找一条无碰撞路径。

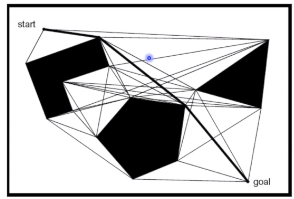
2.可视图法

构建方法

• 找出障碍物的顶点，两两连接，看他们之间是否有障碍物。
• 如果有障碍物，说明不可行。
• 如果没有障碍物，说明是一条可行路径，就将其放入拓扑连通图中，将此顶点作为连通图的顶点。
• 可视图由所有连接可见顶点对的边组成，初始位置和目标位置也作为顶点。

特点

优点

• 简单，环境地图用多边形描述物体时更为方便
• 可得到路径长度长最优的解

缺点

• 所得路径过于靠近障碍物，不够安全

改进

• 以远大于机器人半径的尺寸膨胀障碍物，但容易造成可行路径的消失
• 在路径规划后修改所得路径，使其与障碍物保持一定的距离

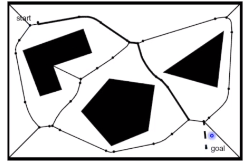
3.Voronoi diagram

构建方法

取障碍物之间的中间点，以最大化机器人和障碍物之间的距离

1. 对于自由空间的每个点，计算他到最近障碍物的距离；
2. 在垂直于二维空间平面的轴上用高度表示该点到障碍物的距离，类似于画直方图；
3. 当某个点到两个障碍物或多个障碍物的距离相等时，距离点处出现尖峰，把这些尖峰点连起来就构成了Voronoi diagram。

特点

优点

• 安全性高

缺点

• 计算复杂，路径长度较可视图法长，不适用于短距离的定位传感器

单元分解法

1.基本思想

• 将位形空间的自由空间分为若干的小区域，每个区域作为一个单元
• 以单元为顶点，以单元之间的相邻关系为边构成一张连通图
• 在连通图中寻找包含初始姿态和目标姿态的单元，搜索连接初始单元和目标单元的路径
• 根据所得路径的单元序列生成单元内部的路径

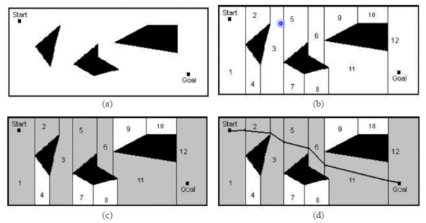
2.精确单元分解

原理

单元边界严格基于环境几何形状分解，所得单元完全空闲

特点

优点

• 机器人无需考虑在每个空闲单元中的具体位置，只需考虑如何从一个单元移动到相邻的空闲单元
• 单元数与环境大小无关

缺点

• 计算效率极大依赖于环境中物体的复杂度

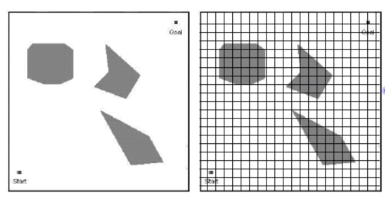
3.近似单元分解

原理

• 栅格表示法：把环境分解成若干个大小相同的栅格
• 用栅格的自由或被占，表示是自由空间还是障碍空间
• 并不是每个单元都完全空闲或完全被占，因此是对实际地图的一种近似

特点

优点

• 非常简单，与环境的疏密和物体形状的复杂度无关

缺点

• 对存储空间要求较大

改进

• 四叉树表示法：递归地把环境分为4个大小相等的子区域，直到每个区域中所包含的基本元素全为0或全为1
• 判断相邻单元时较为困难

人工势场法（Artificial Potential Field）

基本思想

• 构建虚拟势场，目标点对机器人产生吸引力，障碍物对机器人产生排斥力
• 所有力的合成构成机器人的控制律

1.构建人工势场

目标点的吸引势场：

• 离目标点越近吸引力越小

$$U_{att}(\mathbf{x})=\left\{\begin{array}{cc} K_{a}\left|\mathbf{x}-\mathbf{x}_{d}\right|^{2} & \left|\mathbf{x}-\mathbf{x}_{d}\right| \leq d_{a} \\ K_{a}\left(2 d_{a}\left|\mathbf{x}-\mathbf{x}_{d}\right|-d_{a}^{2}\right) & \left|\mathbf{x}-\mathbf{x}_{d}\right|>d_{a} \end{array}\right.$$

• $K_a$为系数
• $\mathbf{x}$ 为被评估点
• $\mathbf{x}_d$ 为目标点
• $d_a$ 为距离阈值

障碍物的推斥势场

• 离障碍物越近排斥力越大

$$U_{rep}(\mathbf{x})=\left\{\begin{array}{cc} \frac{1}{2} K_{r}\left(\frac{1}{\rho}-\frac{1}{\rho_{0}}\right)^{2} & \rho \leq \rho_{0} \\ 0 & \rho>\rho_{0} \end{array}\right.$$

• $\rho$为被评估点和障碍点之间的距离
• $\rho_0$为预定义的距离阈值

2.根据势场计算力

• 对势场求偏导数

$$F_{att}(\mathbf{x})=-\nabla U_{att}(\mathbf{x})=\left\{\begin{array}{cc} -2 K_{a}\left(\mathbf{x}-\mathbf{x}_{d}\right) & \left|\mathbf{x}-\mathbf{x}_{d}\right| \leq d_{a} \\ -2 K_{a} d_{a} \frac{\mathbf{x}-\mathbf{x}_{d}}{\left|\mathbf{x}-\mathbf{x}_{d}\right|} & \left|\mathbf{x}-\mathbf{x}_{d}\right|>d_{a} \end{array}\right.$$ $$F_{rep}(\mathbf{x})=-\nabla U_{rep}(\mathbf{x})=\left\{\begin{array}{cc} K_{r}\left(\frac{1}{\rho}-\frac{1}{\rho_{0}}\right) \frac{1}{\rho^{2}} \frac{\partial \rho}{\partial \mathbf{x}} & \rho \leq \rho_{0} \\ 0 & \rho>\rho_{0} \end{array}\right.$$ $$\frac{\partial \rho}{\partial \mathbf{x}}=\left(\frac{\partial \rho}{\partial x} \frac{\partial \rho}{\partial y}\right)^{T}=\frac{\mathbf{x}-\mathbf{x}_{0}}{\rho}$$

其中$\mathbf{x}_0$是最近障碍物的坐标向量

3.计算合力

• 计算吸引力和排斥力的合力，进而由力计算得到控制律
• 力的方向就是机器人的运动方向，大小可以对应加速度控制

$$\begin{aligned} F(\mathbf{x}) &=-\nabla U(\mathbf{x}) \\ &=-\nabla U_{a t t}(\mathbf{x})-\nabla U_{rep}(\mathbf{x}) \\ &=F_{a t t}(\mathbf{x})+F_{r e p}(\mathbf{x}) \end{aligned}$$

4.特点

• 机器人是人工势场影响的一个点，沿着势场方向就可以避开障碍物到达目标点
• 所构建的势场构成了机器人的控制律，能够较好地适应目标的变化和环境中的动态障碍物，可以作为实时避障算法

缺点

• 存在局部最小，容易震荡和死锁