机器人路径规划算法（三）最优路径搜索算法

在形成的连通图中搜索最优路径

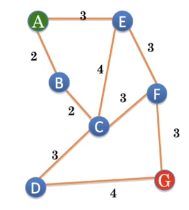
可视图法节点对应的是障碍物的顶点，边对应的是障碍物间可通行的路径
单元分解法节点对应的是区域，边对应的区域的单元间的路径

简介

精确算法

生成精确的最优点
深度优先法、广度优先法
遍历获得所有路径后选择最优解
优化：优先级定义的广度优先法、Dijstra算法
存在问题：耗时，难以满足机器人在线快速规划要求

近似算法

近似最优搜索：
- 启发式搜索：$ A^{} $，$ D^{} $
- 准启发式搜索：退火、进化、蚁群优化等

1.深度优先法

原理

从起始节点开始按深度方式依次探索节点未被访问过的相邻节点
在一个相邻节点被访问之后，优先访问该节点的下一个未被访问的相邻节点，直到扩展图的最深层，即没有可访问的后继节点，或者到达目标节点
返回上一层，探索该节点的其他未被访问的相邻节点

示意

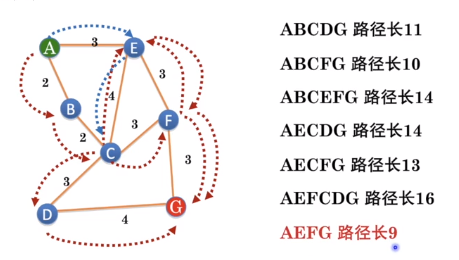
特点

可能会访问已经访问过的节点，或者进入冗余路径

2.优先级定义的广度优先法

原理

从起始节点开始访问该节点所有未曾访问过的相邻节点
从这些相邻节点出发依次访问他们的相邻节点
先被访问节点的相邻节点优先于后被访问节点的相邻节点
直到所有的被访问的节点的相邻节点都被访问到

示例

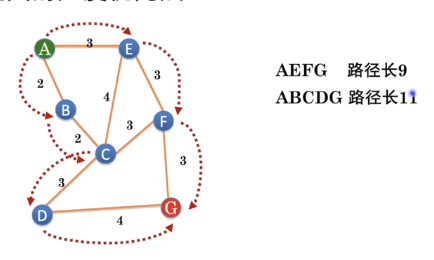
特点

由于算法定义了访问优先级，因此不会遍历所有路径
但可能会导致搜索不到最短路径

3.Dijkstra算法

原理

采用优先级定义的广度优先搜索思想，优先级依据路径长度定义
以起始点为中心按路径长度递增方式层层向外扩展。直到扩展到终止点
设置两个集合S和T，S存放已经找到最短路径的顶点，T是尚未确定路径的顶点集合，同时也描述了起始点经过集合S中的顶点到该点的最短路径及长度。
每次更新时，从T中找出路径最短的点加入集合S中
T中顶点最短路径及长度则根据加入点作为中间点后起始点到该点距离是否减小来判断是否更新

示例

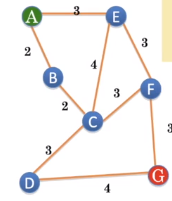
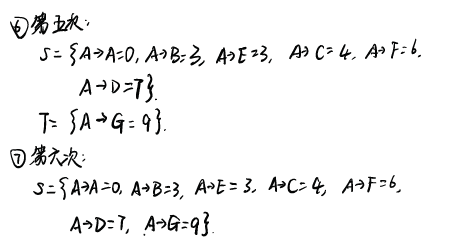
特点

避免路径的遗漏问题规模大时搜索比较费时

4.A*算法

There’s a tradeoff between planning with pathfinders and reacting with movement algorithms. Planning generally is slower but gives better results; movement is generally faster but can get stuck. If the game world is changing often, planning ahead is less valuable. I recommend using both: pathfinding for big picture, slow changing obstacles, and long paths; and movement for local area, fast changing, and short paths.

原理

基于优先级定义的广度优先搜索
根据启发式评估函数在连通图中寻找最优路径
选择路径代价最小的节点作为下一步的探索节点进行跳转

评估函数定义如下 $f(n) = g(n) + h(n)$

$n$表示节点
$g(n)$表示从起始点到当前节点的实际代价
$h(n)$为当前节点到目标点的最佳路径的估计代价

相关概念

搜索区域（The Search Area）：图中的搜索区域被划分为了简单的二维数组，数组每个元素对应一个小方格，当然我们也可以将区域等分成是五角星，矩形等，通常将一个单位的中心点称之为搜索区域节点（Node）。　　
开放列表(Open List)：我们将路径规划过程中待检测的节点存放于Open List中，而已检测过的格子则存放于Close List中。
父节点（parent）：在路径规划中用于回溯的节点，开发时可考虑为双向链表结构中的父结点指针。
路径排序（Path Sorting）：具体往哪个节点移动由以下公式确定：F(n) = G + H 。G代表的是从初始位置A沿着已生成的路径到指定待检测格子的移动开销。H指定待测格子到目标节点B的估计移动开销。
启发函数（Heuristics Function）：H为启发函数，也被认为是一种试探，由于在找到唯一路径前，我们不确定在前面会出现什么障碍物，因此用了一种计算H的算法，具体根据实际场景决定。在我们简化的模型中，H采用的是传统的曼哈顿距离（Manhattan Distance），也就是横纵向走的距离之和
流程

把起点加入 open list 。
重复如下过程：

遍历open list ，查找F值最小的节点，把它作为当前要处理的节点，然后移到close list中
对当前方格的 8 个相邻方格一一进行检查，如果它是不可抵达的或者它在close list中，忽略它。否则，做如下操作：
- 如果它不在open list中，把它加入open list，并且把当前方格设置为它的父亲
- 如果它已经在open list中，检查这条路径 ( 即经由当前方格到达它那里 ) 是否更近。如果更近，把它的父亲设置为当前方格，并重新计算它的G和F值。如果你的open list是按F值排序的话，改变后你可能需要重新排序。
遇到下面情况停止搜索：
- 把终点加入到了 open list 中，此时路径已经找到了，或者
- 查找终点失败，并且open list 是空的，此时没有路径。

从终点开始，每个方格沿着父节点移动直至起点，形成路径。

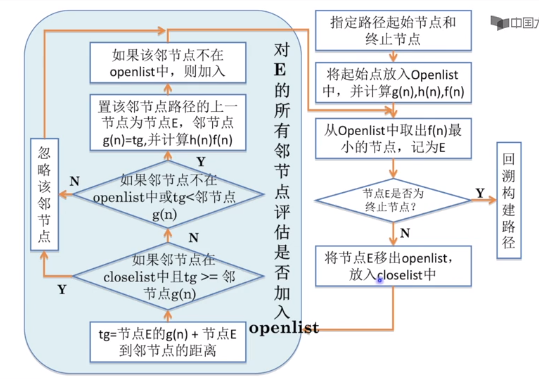
伪代码

function A*(start, goal)
    // The set of nodes already evaluated.
    closedSet := {}
    // The set of currently discovered nodes still to be evaluated. Initially, only the start node is known.
    openSet := {start}
    // For each node, which node it can most efficiently be reached from.
    // If a node can be reached from many nodes, cameFrom will eventually contain the most efficient previous step.
    cameFrom := the empty map

    // For each node, the cost of getting from the start node to that node.
    gScore := map with default value of Infinity
    // The cost of going from start to start is zero.
    gScore[start] := 0
    // For each node, the total cost of getting from the start node to the goal
    // by passing by that node. That value is partly known, partly heuristic.
    fScore := map with default value of Infinity
    // For the first node, that value is completely heuristic.
    fScore[start] := heuristic_cost_estimate(start, goal)

    while openSet is not empty
        current := the node in openSet having the lowest fScore[] value
        if current = goal
            return reconstruct_path(cameFrom, current)

        openSet.Remove(current)
        closedSet.Add(current)
        for each neighbor of current
            if neighbor in closedSet
                continue        // Ignore the neighbor which is already evaluated.
            // The distance from start to a neighbor
            tentative_gScore := gScore[current] + dist_between(current, neighbor)
            if neighbor not in openSet    // Discover a new node
                openSet.Add(neighbor)
            else if tentative_gScore >= gScore[neighbor]
                continue        // This is not a better path.

            // This path is the best until now. Record it!
            cameFrom[neighbor] := current
            gScore[neighbor] := tentative_gScore
            fScore[neighbor] := gScore[neighbor] + heuristic_cost_estimate(neighbor, goal)

    return failure


function reconstruct_path(cameFrom, current)
    total_path := [current]
    while current in cameFrom.Keys:
        current := cameFrom[current]
        total_path.append(current)
    return total_path

示意

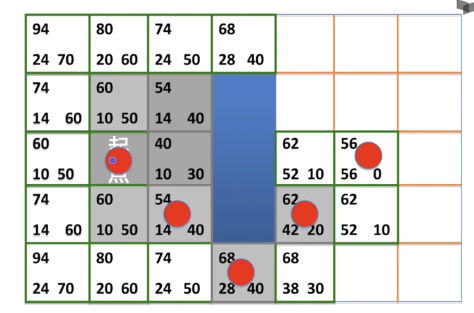
实际成本是欧式距离
预估成本是曼哈顿距离

5.蚁群算法

用一个蚂蚁的行走路径表示待优化问题的一个可行解
用整个蚂蚁群体的所有路径作为待优化问题的解空间
用蚂蚁群体收敛选择的路径作为问题的优化解

实现方式

每个蚂蚁在经过的路上释放信息素，称为正反馈

$\boldsymbol{\tau}_{i j}(\boldsymbol{t}) \leftarrow \boldsymbol{\tau}_{i j}(\boldsymbol{t})+\boldsymbol{\Delta} \boldsymbol{\tau}$

信息素与路径长度成反比
$\Delta_{\tau}$ 可以是经过该路段留下的实时信息素，也可以是到达目标点后对整段路径留下的信息素
为避免早熟收敛，信息素采用挥发机制

$\tau \leftarrow(1-\rho) \tau, \rho \in[0,1]$

信息素计算总表达式

$\begin{array}{c} \boldsymbol{\tau}_{i j}(\boldsymbol{t}+\boldsymbol{n})=(\mathbf{1}-\boldsymbol{\rho})^{n} \boldsymbol{\tau}_{i j}(\boldsymbol{t})+\boldsymbol{\Delta} \boldsymbol{\tau}_{i j}(\boldsymbol{t}+\boldsymbol{n}) \\ \Delta \boldsymbol{\tau}_{i j}(\boldsymbol{t}+\boldsymbol{n})=\sum_{k=1}^{m} \boldsymbol{\Delta} \tau_{i j}^{k}(\boldsymbol{t}+\boldsymbol{n}) \end{array}$

$m$ 为蚂蚁总数，$k$ 为蚂蚁编号，$\Delta_{ij}^k(t+n)$表示在n时间内第k个蚂蚁在路径$ij$上留下的信息素

每个蚂蚁根据后续可选边的评估概率决策

$p_{i j}^{k}(t)=\left\{\begin{array}{cc} \frac{a_{i j}(t)}{\sum_{k \in N_{i}^{k}} a_{i l}(t)} & \text { if } j \in N_{i}^{k} \\ 0 & \text { if not } \end{array}\right.$

$N_i^k$为第k个蚂蚁当前节点i的相邻节点集合，$a_{ij}(t)$为节点$i$的路径评估值。计算如下：

特点

通过局部探测加记忆机制来搜索可行解
优点
- 问题的图表示随着最优化同步变化，可适应问题的动态性
- 可实现并行计算
缺点
- 计算量大，耗时长
- 参数需依靠经验反复调试，不同环境适配不同参数

上篇机器人路径规划算法（二）拓扑连通图的构建方法1

下篇机器人路径规划算法（四）PRM系列

简介