PRM(Probabilistic RoadMap)

基本思想

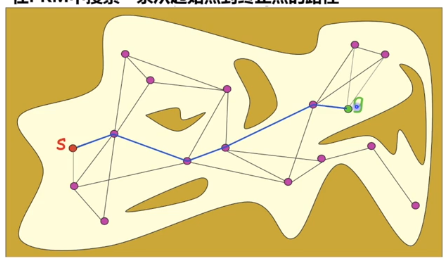
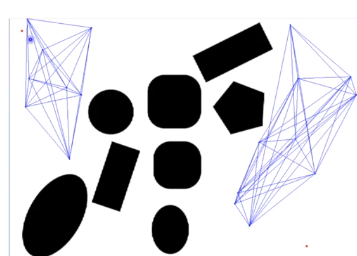
通过随机采样和碰撞检测找到自由位形空间中的路径点和无碰路径，构成连通图

• 在位形空间坐标系中随机取点
• 对采样的点进行碰撞检测，把无碰撞姿态作为图节点
• 每个图节点和其最近相邻的k个节点直线连接，保留无碰路径作为图的边
• 加入起始点和终止点构成RoadMap
• 采用基于节点的搜索算法(Dijkstra,A,D)在RoadMap中找到一条代价最小的路径

算法的流程图如下

需考虑的几个问题

• 随机位形选择 采用均匀随机采样方式
• 寻找最近邻点 采用KD树方法加速
• 生成局部路径 在一定范围内直接连接图节点
• 检查路径无碰 可以增量式取点或者二分法取点，判断点是否在障碍物区域内
• 进行路径优化
  • 从目标点开始依次找它前面的点，检测是否发生碰撞
  • 假如未发生碰撞，继续往前寻找，直到路径发生碰撞，将目标点与当前点的上一个点连接
  • 从当前点开始继续此优化过程
• 非全联通情况
  • 环境复杂，存在狭窄通道等困难场景时，会存在图非联通的情况
  • 对节点进行困难度表示，节点一定距离范围内的节点的倒数、该节点到不与该节点联通的最近连通单元距离倒数、局部路径规划失败率
  • 以困难度作为该节点被选择为扩张节点的概率
  • 选择后，从该节点出发随机选择方向运动，碰到障碍物后再随机选择方向运动，循环若干次直至成功建立与其他联通单元的连接

特点

• 优点
  • 简化了对环境的解析计算，可快速得到行车图
  • 适用于高维自由位形空间中的规划
  • 是近似完备的路径规划
• 缺点
  • 对自由空间连通性表达的完整性依赖于采样次数
  • 难以评估需要多少时间进行充分采样
  • 不考虑机器人的执行可行性

发展趋势

• 将路径规划转为马尔可夫决策问题，采用深度学习/强化学习进行求解。
• 综合考虑与环境中人的交互，学习地图成本，构建成本地图